11 клас. Інформатика. Дистанційне навчання: тест-інтерв'ю з теми "АЛГОРИТМИ"

Тестування з теми АЛГОРИТМИ

Інтерактивна вправа «Допуск до тесту».

Запитання для самоперевірки:

1)Що таке алгоритм? Наведіть приклади подій, які не є алгоритмічними.
Алгори́тм (латинізов. Algorithmi за араб. ім'ям узб. математика аль-Хорезмі) — набір інструкцій, які описують порядок дій виконавця, щоб досягти результату розв'язання задачі за скінченну кількість дій; система правил виконання дискретного процесу, яка досягає поставленої мети за скінченний час. Для візуалізації алгоритмів часто використовують блок-схеми.

2) Хто або що може бути виконавцем алгоритму? Наведіть приклади виконавців.
В сучасному світі виконавцем алгоритму при будь-якій діяльності у формалізованому аспекті складає основу отримання освіти або навчання на прикладах: сумлінних учнів, зразкових студентів, початківців-програмістів, ЕОМ, та інших живих і неживих істот.

3)Які ви знаєте форми подання алгоритму? Наведіть приклади різних форм алгоритму.
Поняття алгоритму належить до підвалин математики. Обчислювальні процеси алгоритмічного характеру (як-то арифметичні дії над цілими числами, знаходження НСД двох чисел тощо) відомі людству з глибокої давнини. Проте, чітке поняття алгоритму сформувалося лише на початку XX століття. Таким чином: маємо словесну форму запису рецептів; формульну форму запису уматематиці, фізиці, хімії; форма запису у вигляді блок-схем; у вигляді штучних мов програмування для ЕОМ; у вигляді нотних партитур для виконавців музики і так далі.

4) Яка форма подання алгоритму є найзручнішою? Чому?
Найзручніше, для ЕОМ, це штучна мова кодування алгоритмів, яка дає можливість знаходити прогнозувати майбутнє. Найзручніше, для учнів, формульно-словесна форма або блок-схеми.

5) Чи можна уявити життя без виконання алгоритмів?
На основі подібності алгоритмів різних сфер діяльності була сформована концепція (теорія) експертних систем. А без експертних систем сучасне життя людей у інформаційному суспільстві не піддається хоч якомусь системному упорядкуванню, організованості!!!

6) Що таке програма?
Під впливом досліджень в галузі штучного інтелекту розроблено парадигму логічного програмування. На відміну від імперативної та функційної парадигм, логічне програмування не вимагає від розробника описувати спосіб розв'язання поставленої задачі. Planner — перша мова логічного програмування, була розроблена в 1969 році. На початку 1970-х був розроблений Пролог, який згодом став найпоширенішою мовою логічного програмування зі стандартом ISO, затвердженим у 1995 році^[9] . Отже, програма - це нотації віртуальних подій для інтерпретації фізичним виконавцем. До речі, перша мова програмування, Планкалькуль^[en] (нім. Plankalkül) була розроблена Конрадом Цузе в 1946 році, але через відсутність компіляторів виконання написаних цією мовою програм було неможливим.

7) Що таке середовище виконання алгоритму?

Розробка алгоритмічних мов для програмування обчислювальних пристроїв розпочалась в 1951 році з публікації німецького інженера Ганса Рутісхаузера^[en] (нім. Heinz Rutishauser). Спочатку важливою здавалась проблема нотації, її досліджував Олексій Ляпунов, але поступово вона відійшла на другий план. Кожен алгоритм передбачає існування початкових (вхідних) даних та в результаті роботи призводить до отримання певного результату. Робота кожного алгоритму відбувається шляхом виконання послідовності деяких елементарних дій. Ці дії називають кроками, а процес їхнього виконання називають алгоритмічним процесом. В такий спосіб відзначають властивість дискретності алгоритму^[10].

7б) Що таке властивість алгоритму?

Важливою властивістю алгоритмів є масовість, або можливість застосування до різних вхідних даних. Тобто, кожен алгоритм покликаний розв'язувати клас однотипних задач.

Необхідною умовою, яка задовольняє алгоритм, є детермінованість, або визначеність. Це означає, що виконання команд алгоритму відбувається у єдиний спосіб та призводить до однакового результату для однакових вхідних даних.

Вхідні дані алгоритму можуть бути обмежені набором припустимих вхідних даних. Застосування алгоритму до неприпустимих вхідних даних може призводити до того, що алгоритм ніколи не зупиниться, або потрапить в тупиковий стан (зависання) з якого не зможе продовжити виконання.

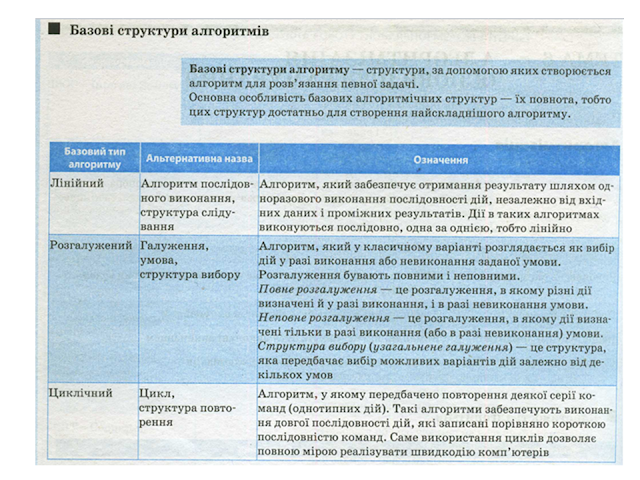
8) Які бувають структури алгоритму?
Формалізація поняття алгоритму дозволила дослідити існування задач, для яких не існує алгоритмів пошуку розв'язків. Згодом було доведено неможливість алгоритмічного обчислення розв'язків ряду задач, що робить неможливим їхнє розв'язання на будь-якому обчислювальному пристрої. Отже, структури алгоритмів бувають шість видів.

9) Що означає структура слідування?
Структура слідування - це послідовне виконання нотацій виконавцем алгоритму, при якому він не повертається у попередній стан, і при якому не виконує вибору із множини дій згідно умовних нотацій чи різних станів виконавця.

10)Чи може в структурі слідування якась команда починатися словом «якщо»?
Не може!

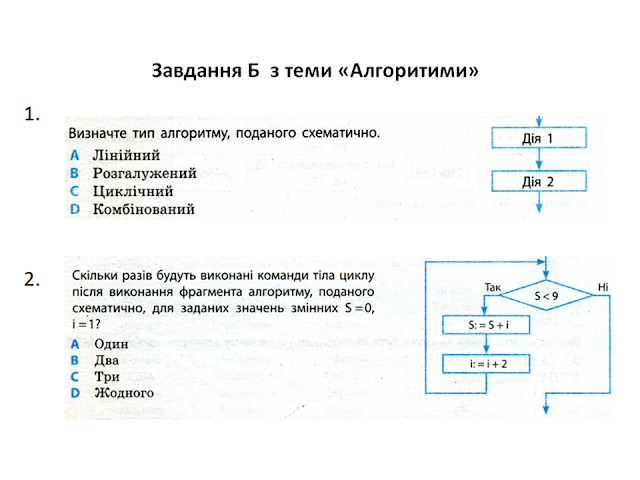
11)Наведіть приклад алгоритму, який називаємо а)лінійним; б)складеним(розгалуженим); в) циклічним(з повторенням)?

12)Які математичні відношення використовуються в умовних операторах?

Найбільш наочний приклад відношення еквівалентності — поділ учнів школи на класи.
Відношення рівності (« $\;=$ », <, >, ) тривіальне відношення еквівалентності на довільній множині, зокрема на множині дійсних чисел.
Порівняння по модулю, («а ≡ b (mod n)»).
В Евклідовій геометрії
- Відношення конгруентності (« $\cong$ »).
- Відношення подібності (« $\ \sim$ »).
- Відношення паралельності прямих (« $\|$ »).
Відношення рівнопотужності множин є відношенням еквівалентності.
Еквівалентність функцій в математичному аналізі:

13)В яких випадках застосовують алгоритми з розгалуженням?
Використання алгоритмів для евристичного пошуку чи вибору із наявної множини, чи пошуку на графі виграшної стратегії в складніших задачах та іграх (шашки, шахи) майже не реальний. За деякими оцінками ігрове дерево гри в шашки містить 10⁴⁰ вершин, в шахах 10¹²⁰ вершин. Якщо при грі в шашки для однієї вершини потрібно 1/3 наносекунди, то всього ігрового часу буде потрібно 1021 століть. У таких випадках вводяться штучні умови зупинки, засновані на таких факторах, як найбільша допустима глибина вершин у дереві пошуку або обмеження на час і обсяг пам'яті. Наприклад, шаховий комп'ютер Deep Blue (який виграв у Гарі Каспарова) для глибини у 12 ходів перебравши усі можливі стани, тоді застосував евристичні функції оцінки.

14)Які оператори називають умовно-продуктивними?
Продуктивність простого алгоритму з умовами мінімаксу (тобто, накладається умова вибору найменшого та найбільшого значення) може бути значно покращено, не впливаючи на результат, за допомогою відсічення альфа-бета. Теоретично, це еквівалент алгоритму мінімаксу, за допомогою якого завжди виходить такий же результат, але помітно швидше, так як цілі частини дерева виключаються без проведення аналізу. В основі цієї процедури лежить ідея Дж. Маккарті про використання двох змінних, позначених α і β (1961 рік). найменшета найбільше із усіх реалізованих виконавцем значення.

Інші методи евристичних відсікань також можуть бути використані, але не всі з них гарантовано дають той же результат, що й алгоритм без відсікань.

Простий алгоритм мінімаксу може бути тривіально змінений, щоб додатково повертати саму стратегію разом з результатом мінімаксу.
15)Подайте приклади використання умовного оператора у скороченій формі?

Приклад

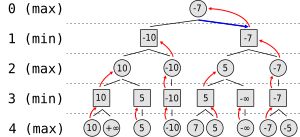
Припустимо, що в грі є максимум два можливих кроки для кожного гравця на кожен хід. Алгоритм генерує дерево праворуч, де кола є ходи максимізуючого гравця, а квадрати являють собою ходи суперника ( мінімізуючий гравець ). Через обмеженість обчислювальних ресурсів, як описано вище, дерево обмежено на 4 кроки уперед.

Алгоритм оцінює кожен вузол за допомогою евристичних функцій оцінки, отримані значення показано на малюнку. Ходи, де максимізуючий гравець виграє, оцінені як додатна нескінченність, в той час як кроки, які приведуть до перемоги мінімізуючого гравця, оцінені як від'ємна нескінченність. На рівні 3 алгоритм буде вибирати, для кожного вузла, найменше зі значень його дочірніх вузлів, і призначить це значення тому ж вузлу (наприклад, вузол зліва буде вибирати мінімальне з "10" і "+ ∞", тому призначить собі значення "10"). Наступний крок, на рівні 2, полягає у виборі найбільшого значення для кожного вузла серед його дочірніх вузлів. Знову ж таки, кожне значення присвоюється кожному батьківському вузлу. Алгоритм продовжує оцінки максимального і мінімального значень дочірніх вузлів по черзі, аж поки не досягне кореневого вузла, де він вибирає хід з найбільшим значенням (представлено на малюнку синьою стрілкою). Це крок, який гравець повинен зробити для того, щоб звести до мінімуму максимально можливої втрати.

16)Подайте приклади використання умовного оператора у повній формі?

Наприклад, у філософії термін «максиміна» часто використовується в контексті «Теорії справедливості» Джона Роулза, де він ставиться до нього (Rawls (1971, с. 152)) в контексті принципу різниці. Роулз визначив цей принцип як правило, яке свідчить, що соціальні і економічні нерівності повинні бути організовані так, що «вони повинні мати найбільшу користь найменш сприятливому члену суспільства». Іншими словами, нерівномірний розподіл може бути тільки тоді, коли він максимізує мінімальну користь тих, хто має низький рівень добробуту (які він називає «сировинні товари»). Це приклад, де умовний оператор максимізує мінімальну користь.