Лекція 4.4. Розв’язування типових математичних задач засобами табличного процесора
1. Задача підбору параметрів
Означення. Задачею підбору параметра називається знаходження такого значення аргумента даної функції, при якому ця функція набуває заданого значення.
Зокрема, це може бути пошук коренів заданого рівняння f(x)=0, коли необхідно знайти такі значення аргумента, за яких функція набуває нульового значення.
Розглянемо задачу знаходження коренів рівняння 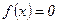 . Якщо
. Якщо 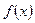 має простий вигляд, то корені можна знайти аналітичним методом, тобто за формулами:
має простий вигляд, то корені можна знайти аналітичним методом, тобто за формулами:
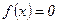 . Якщо
. Якщо 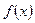 має простий вигляд, то корені можна знайти аналітичним методом, тобто за формулами:
має простий вигляд, то корені можна знайти аналітичним методом, тобто за формулами:
q при 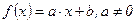 маємо лінійне рівняння
маємо лінійне рівняння 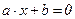 , корінь якого
, корінь якого 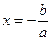 ;
;
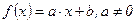 маємо лінійне рівняння
маємо лінійне рівняння 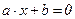 , корінь якого
, корінь якого 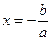 ;
;
q при 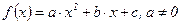 маємо квадратне рівняння
маємо квадратне рівняння 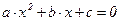 , дійсні корені якого
, дійсні корені якого 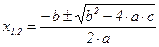 .
.
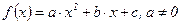 маємо квадратне рівняння
маємо квадратне рівняння 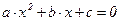 , дійсні корені якого
, дійсні корені якого 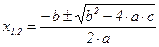 .
.
Але у більш складних випадках формул для обчислення коренів рівняння 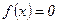 не існує. Тому застосовують наступну чисельну методику:
не існує. Тому застосовують наступну чисельну методику:
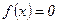 не існує. Тому застосовують наступну чисельну методику:
не існує. Тому застосовують наступну чисельну методику:
q спочатку здійснюють відокремлення всіх коренів, тобто на заданому широкому проміжку 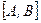 для кожного кореня знаходять досить вузький проміжок
для кожного кореня знаходять досить вузький проміжок 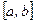 , на якому відсутні інші корені;
, на якому відсутні інші корені;
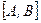 для кожного кореня знаходять досить вузький проміжок
для кожного кореня знаходять досить вузький проміжок 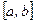 , на якому відсутні інші корені;
, на якому відсутні інші корені;
q уточнюють корені, тобто на кожному з вузьких проміжків знаходять значення кореня із заданою точністю.
Розглянемо відокремлення коренів. Основні методи відокремлення коренів: графічний та табличний.
У відповідності з графічним методом необхідно побудувати графік заданої функції 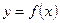 на всьому заданому проміжку
на всьому заданому проміжку 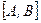 , після чого візуально локалізувати точки його перетину з віссю Ox. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки
, після чого візуально локалізувати точки його перетину з віссю Ox. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки 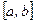 так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу – його громіздкість. Другий недолік – ненадійність – пов’язаний з можливістю втратити корені при неякісній побудові графіка.
так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу – його громіздкість. Другий недолік – ненадійність – пов’язаний з можливістю втратити корені при неякісній побудові графіка.
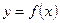 на всьому заданому проміжку
на всьому заданому проміжку 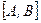 , після чого візуально локалізувати точки його перетину з віссю Ox. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки
, після чого візуально локалізувати точки його перетину з віссю Ox. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки 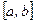 так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу – його громіздкість. Другий недолік – ненадійність – пов’язаний з можливістю втратити корені при неякісній побудові графіка.
так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу – його громіздкість. Другий недолік – ненадійність – пов’язаний з можливістю втратити корені при неякісній побудові графіка.
Більш зручним слід вважати табличний метод, оскільки він досить формальний і зводиться до послідовності простих обчислювальних операцій. У відповідності з цим методом, на всьому широкому проміжку 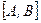 визначають знаки функції
визначають знаки функції 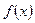 з певним кроком h. З одержаної таблиці знаків вибирають вузькі проміжки
з певним кроком h. З одержаної таблиці знаків вибирають вузькі проміжки 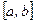 , на кінцях яких функція має протилежні знаки. Чим дрібніший крок h, тим надійніше будуть відокремлені корені, тим менша ймовірність їх втратити.
, на кінцях яких функція має протилежні знаки. Чим дрібніший крок h, тим надійніше будуть відокремлені корені, тим менша ймовірність їх втратити.
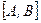 визначають знаки функції
визначають знаки функції 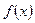 з певним кроком h. З одержаної таблиці знаків вибирають вузькі проміжки
з певним кроком h. З одержаної таблиці знаків вибирають вузькі проміжки 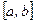 , на кінцях яких функція має протилежні знаки. Чим дрібніший крок h, тим надійніше будуть відокремлені корені, тим менша ймовірність їх втратити.
, на кінцях яких функція має протилежні знаки. Чим дрібніший крок h, тим надійніше будуть відокремлені корені, тим менша ймовірність їх втратити.
Приклад. Відокремимо корені рівняння 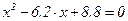 на широкому проміжку
на широкому проміжку 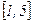 . Виберемо крок
. Виберемо крок 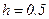 . При цьому ми припускаємо, що відстань між найближчими коренями даного рівняння перевищує вибраний крок, і тому корені втрачені не будуть. Складемо таблицю знаків функції
. При цьому ми припускаємо, що відстань між найближчими коренями даного рівняння перевищує вибраний крок, і тому корені втрачені не будуть. Складемо таблицю знаків функції 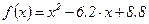 на проміжку
на проміжку 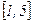 .
.
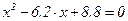 на широкому проміжку
на широкому проміжку 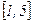 . Виберемо крок
. Виберемо крок 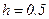 . При цьому ми припускаємо, що відстань між найближчими коренями даного рівняння перевищує вибраний крок, і тому корені втрачені не будуть. Складемо таблицю знаків функції
. При цьому ми припускаємо, що відстань між найближчими коренями даного рівняння перевищує вибраний крок, і тому корені втрачені не будуть. Складемо таблицю знаків функції 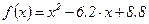 на проміжку
на проміжку 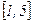 .
.| x | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 |
| Знак f(x) | + | + | + | – | – | – | + | + |
Таким чином, таблиця показує, що на широкому проміжку 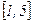 знаходяться два корені: перший – в межах вузького проміжка
знаходяться два корені: перший – в межах вузького проміжка 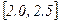 , другий – в межах вузького проміжка
, другий – в межах вузького проміжка 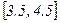 .
.
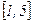 знаходяться два корені: перший – в межах вузького проміжка
знаходяться два корені: перший – в межах вузького проміжка 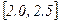 , другий – в межах вузького проміжка
, другий – в межах вузького проміжка 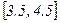 .
.
Подібну таблицю для заданої функції 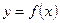 можна скласти засобами MS Excel. Для цього достатньо знати широкий проміжок
можна скласти засобами MS Excel. Для цього достатньо знати широкий проміжок 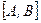 , а також правильно вибрати крок побудови таблиці h.
, а також правильно вибрати крок побудови таблиці h.
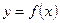 можна скласти засобами MS Excel. Для цього достатньо знати широкий проміжок
можна скласти засобами MS Excel. Для цього достатньо знати широкий проміжок 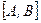 , а також правильно вибрати крок побудови таблиці h.
, а також правильно вибрати крок побудови таблиці h.
Для уточнення коренів в MS Excel використовують підбір параметрів. При цьому порядок дій для кожного вузького проміжка 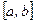 може бути наступним:
може бути наступним:
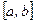 може бути наступним:
може бути наступним:
¨ Вибрати комірки для розміщення значення аргумента x і функції y (наприклад, A1 і A2 відповідно).
¨ В комірку A1 ввести орієнтовне значення кореня. Це має бути один із кінців вузького проміжка 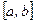 .
.
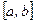 .
.
¨ В комірку A2 ввести формулу для обчислення значення функції 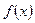 , вважаючи, що аргумент x знаходиться в комірці A1.
, вважаючи, що аргумент x знаходиться в комірці A1.
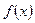 , вважаючи, що аргумент x знаходиться в комірці A1.
, вважаючи, що аргумент x знаходиться в комірці A1.
¨ Виконати команду Сервис-Подбор параметра.... Внаслідок цього на екрані з’являється діалогове вікно Подбор параметра.
¨ В поле Установить в ячейке: ввести адресу комірки значення функції, тобто A2.
¨ В поле Значение: ввести нульове значення.
¨ В поле Изменяя значение ячейки: ввести адресу комірки значення аргумента, тобто A1.
¨ Натиснути кнопку OK діалогового вікна. З’являється нове вікно Результат подбора параметра, в якому повідомляється, вдалося чи ні розв’язати рівняння.
¨ Значення кореня рівняння з’являється у комірці A1.
Якщо користувача не задовольняє точність знайденого значення, то він може її змінити. Для цього треба виконати команду Сервис-Параметры..., у діалоговому вікніПараметры вибрати вкладинку Вычисления, а полі Относительная погрешность: цієї вкладинки ввести інше значення (наприклад, 0.00001 замість 0.001).
Немає коментарів:
Дописати коментар